Solutions to Exercise 1: REPL and standard Python programming

Exercise 1: Use of REPL

The screen shot shows the REPL session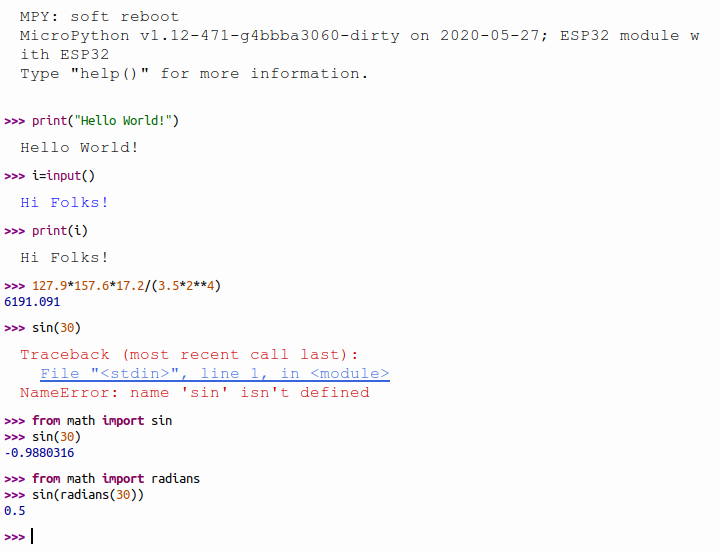

Exercise 2: A simple calculator

In the first example we use fixed values for the calculations. To print out the results I first use integer (%d) format and then floating point format (%f) to get the division right.

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/calculatorV1.py.txt

In the second example I define 4 functions for the 4 basic arithmetic operations. The dictionary with the operator as key and the function as value allows me to select the function to be called depending on the operator given. I write a simple parser to check that user input is correct. Since I force a space between operands and operator it becomes easy to split the calculation into 3 tokens: 2 operands and the operator. Now all I need to do is converting the operator strings to floating values and call the corresponding function.

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/calculatorV2.py.txt

The last example is quite a bit more tricky as I cannot use the string method split to separate operands and operator any more. The parser allows the characters 0..9,"." and "+","-","*","/".

The operator may only consist of 1 or more digits and/or the decimal point. It may not contain more than 1 decimal point and it must contain at least 1 digit. The operator can be only one of the above basic arithmetic operators. Here is my solution. Test it yourself and try to find an illegal character combination that is not treated. Error handling is often the most difficult part of a program!

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/calculatorV3.py.txt

Exercise 3: Conditions

There is nothing much new in this exercise except that it shows how to use conditional statements.

The first version uses the fixed values 5 and 7:

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/conditionsV1.py.txt

The second version takes user input, splits it along spaces and makes sure that exactly 2 tokens have been given

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/conditionsV2.py.txt

The third version also checks that the 2 tokens are valid integer numbers

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/conditionsV3.py.txt

Exercise 4: The Fibonacci Series

In this exercise we try to implement a mathematical function. This should allow you to write your own small algorithm and test it. The function you develop here will be used in exercise 6. Again there are 2 versions: The first one calculates the Fibonacci series F(n) where n is given by the user:

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/fibonacciV1.py.txt

while in the second version the user gives a maximum number not to be exceeded.

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/fibonaciiV2.py.txt

Exercise 5: A bit of Mathematics: Calculate the sine function

Here we implement the calculation of the sine function we used with REPL in the first exercise. It shows how use external modules/libraries. This exercise is pretty simple.

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/math.py.txt

Exercise 6: Classes

This exercise is a bit bigger! It shows you how to develop your own modules and your own classes. In addition you may study some interesting mathematical number series. The last 4 series are actually approximations to well known mathematical constants:

• approximation of Euler's number e:
• the Gregory-Leibniz algorithm, an approximation of pi
• The Wallis algorithm, another approximation of pi
• approximation of ln(2)

When trying to get a good approximation for these numbers you will have to calculate a big number of iterations and you may see a difference between running the program on the PC and running it on the ESP32 where you may see this:3.14159 26535 89793 23846

The reason is simple: My PC has 16 GBytes of RAM memory while the ESP32 has 520 kBytes of RAM. When calculating a big number of iterations you will not be able to keep the intermediate results in a list.

For comparison, here are the correct numbers for pi, e and ln(2)

• pi: 3.14159 26535 89793 23846
• e: 2.71828 18284 59045 23536
• ln(2): 0.69314 71805 59945 30941

The other difference is that the ESP32 has no high resolution screen attached to it such that plotting does not make much sense. (TFT screens do exist and can be attached to the ESP32 such that this statement must be taken with a bit of caution)

Here is a plot of the factorial series and the Fibonacci numbers. Since factorial uses multiplication while Fibonacci uses additions, factorial increases much faster.

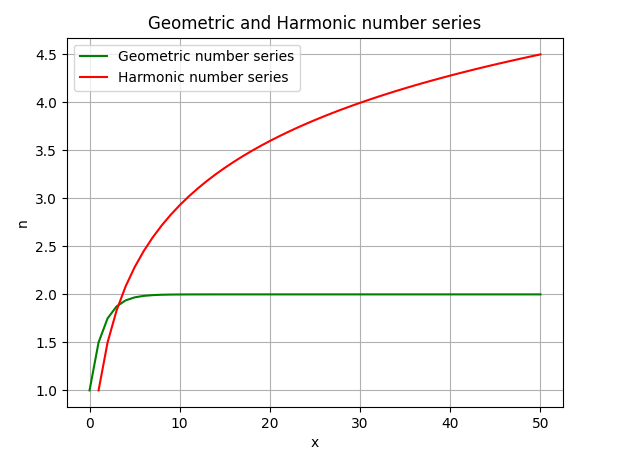
Here a comparison of the geometric and the harmonic number series. As you can easily see geometric series (here with base 2) converges while the harmonic series diverges (albeit slowly).

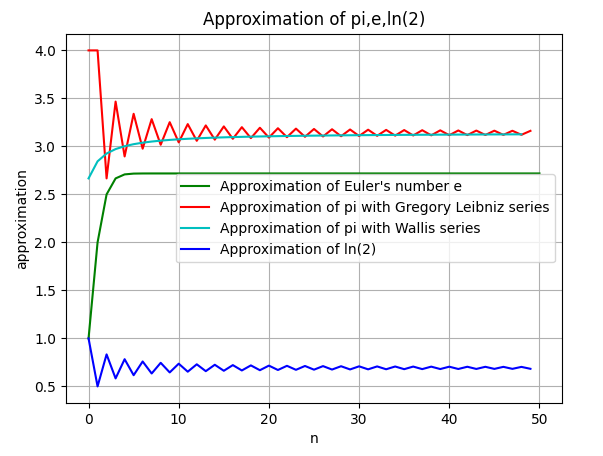
Finally the plot for the approximation of the mathematical constants. You can easily see that the Wallis algorithm converges faster that the Gregory-Leibniz one.

... and here is the code:

First we have the class implementing the calculation of the number series:

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/mathSeries.py.txt

Then the test program, calling each if the methods in the class:

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/mathSeriesTest.py.txt

and finally the program which generates the plots:

https://iotworkshop.africa/pub/IoT_Course_English/SolutionsToREPLAndStandardPythonProgramming/mathSeriesPlot.py.txt

-- Uli Raich - 2020-05-03

Comments